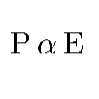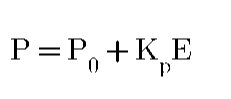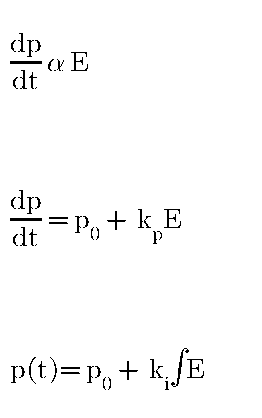PID Controlling mode in automation | Instrumentation blog

PID Controlling mode in automation is explained here in simple terms. Calculations pros and cons included here

This blog contains following topics

• PID Control mode
• P Control mode Drawbacks and calculations
• I Control mode Drawbacks and calculations
• D Control mode Drawbacks and calculations
• How to tuning P [Gain], I [Reset] D[Rate] controls?
• Video - PID Controller in hindi
• PI Control mode
• PD Control mode

Interview Questions from this blog

1. What is full form of PID Controlling?
2. What is Rate control, Reset control and Gain in Controller?
3. How to tune PID Controller?
4. what is  Zeigler Nichols method?
5. How PID Controller works?
6. What is mathematical expression of P I D Control system? 
7. What is error in controller? 

DCS controlling has combination of three modes 

P - Proportional control mode

I - Integral control mode

D - Derivative control mode

Let we see basics of this modes

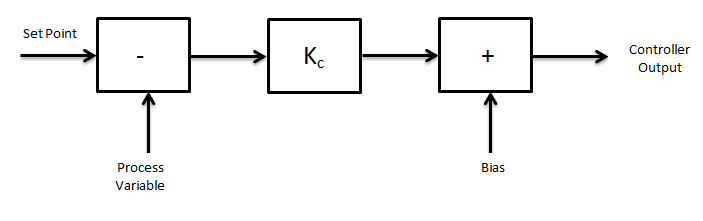
P - Proportional control mode (Gain control) 

Proportional control mode is basic continuous control mode. 

Here Controller output (P) is Proportional to the error (E) 

P = Controller output

This is Set point or required field value which is given by DCS Person

E = Error Value

We can simply say difference between Set point and actual field value.

P0 = Controller output at zero error

Kp = Proportional gain constant

Controller value is equal to error[E] with constant gain[Kp] with output at zero error[P0]. 

P - Proportional control mode (Gain control) 

If Process value [Controller output, P] is equal to set point [ Error, E] then controller value will be zero. Steady state process is not possible so it run smoothly with steady error.

Properties of Proportional mode

• It is Characterized by a continuous linear relationship between input value and output value
• Exhibit offset (Offset means movement from its position example - Car wheel offset is 4 inch means wheel is moving up to 4 inch from his centre with help of Jumper) 
• Lower stability

I - Integral Control Mode (Reset mode) 

In Integral control mode Controller output value is proportional to Error

• P controller exist offset between Process value and set point so I – Integral control mode use becomes useful. Integral control mode eliminates steady state error.

• Integral mode integrate error over a period of time till error reach zero to field controlling devices like Valves, motors, VFDs etc.

• When negative error takes place I mode decreases its output.

Integral control mode

Properties of Integral mode

• Eliminates offset
• It shows oscillatory behavior

Oscillatory behavior = Predictable variation from center point like Current, Voltage

• Large stabilization 

Stabilization = Close enough to its center

D - Derivative control mode ( Rate Control mode) 

Controller output is proportional to the rate of change in error.

Integral control mode cannot predict upcoming behavior of error. When set point is changed it reacts normal.

Derivative control mode solve this problem be resetting whole system. 

Above equation shows controller output depends on rate of change of error with respect to time with multiplied by derivative constant [K_d] with controller output zero. By resetting system it gives kick start for system response.

Reduce Oscillatory behavior 

It provides no output when error is zero

All has individual drawbacks

P - Exhibit offset, Low stability 

I - Oscillatory behavior 

D - No output at zero error

Due to this reason PID is utilities 

PID - Proportional Integral Derivative Control mode. 

It is combined mode of 

P - Proportional Mode, 

I - Integral mode, 

D - Derivative mode

We can clearly see that PID consisting all three Proportional, Integral and Derivative control modes combined. This mode can control Pressure, Temperature, pH, Flow, Redox, Speed, etc.

Example

PID Controlling mode - Proportional integrated derivative control mode example

We can see above example

• This system has PID Controller which gives its output [Level indication control] to control valve.
• Control valve controlling 50% level in tank.
• When level reach 50% Its PV - Process value and SP - Set Point will be same and error between PV and SP will be zero.
• Now PID we scan see 
• When level was 40% Valve opening reduction will start.
• Valve ill not becomes exact zero at 50% but valve opening reduction continued.
• This reduction till level is maintained 50%.
• When level goes below 50% then again valve opening becomes in increasing mode.

How to tuning P [Gain], I [Reset] D[Rate] controls?

1. Trial & Error
2. Process reaction curve technique
3. Zeigler Nichols method

1. Trial & Error – 

A. Adjust Kp

When controlling system activated, suppose controller constants Ki & Kd will be zero and increase proportion term Kp till system oscillations start.

B. Adjust Ki

When system oscillation start Ki adjustment to be done which reduces oscillations.

C. Adjust Kd

When Kp & Ki set, Kd for Fast response.

2. Process reaction curve technique

When controller performances started adjust P [Gain], I [Reset] D [Rate] controls as they gives output. For their output you have to check history curve.

3. Zeigler Nichols method

• This method is for close loop only
• Continuous cycling method and dumped oscillation method procedures for both methods are same but oscillations are different.
• In this method Kp is adjusted till oscillation behavior becomes stable this is called ultimate Period Pu, At this time Ki & kd are zero.
• At stable oscillation constant calling Ultimate gain Ku.
• We can add values of P, PI, PID as below Zeigler Nichols table

PID Tuning - Zeigler Nichols method

Best control mode

Watch Industrial Guide video here

PI - Proportional integrated control mode

This mode is combination of P & I control mode

Mathematical expression of this mode is as below

P = KpE + Kp Ki ∫ Edt + P0

Properties of PI Control mode

• This mode has zero offset
• Maximum deviation produce is larger Proportional controller but lower than integral control mode

PD - Proportional derivative control mode

This mode is combination of Proportional control mode and derivative control mode.

Mathematical expression of PD controller is below

P = KpE + Kp Kd dE/dt + P0

Properties

• Lowest deviation in this control mode
• Small offset
• Lowest stabilization time
• It increases over all stability

Thanks for reading - PID Controlling | Instrumentation blog


Read more Instrumentation blog - Click here
Read more on this topic on Wikipedia - Click here

Naitik Patel
Industrial Guide